2

La calculadora algebraica como herramienta pedagógica para enseñar matemáticas*

 

Bernhard Kutzler

 

 

1. Introducción

 

1.1 La calculadora algebraica

 

Las calculadoras algebraicas son calculadoras gráficas que ofrecen funcionalidades que estaban hasta ahora disponibles solamente en las computadoras. Estas calculadoras pueden simplificar expresiones, derivar, integrar y graficar funciones, resolver ecuaciones, manipular matrices, etc. En pocas palabras: pueden hacer la mayoría de lo que enseñamos en matemáticas en las escuelas y universidades.

 

Hay actualmente dos calculadoras algebraicas en el mercado: la TI-92 y la TI-89. El modelo Casio  CFX-9970 también puede ejecutar un poco de cómputo algebraico, pero no es tan potente como los dos modelos de Texas Instruments. Las siguientes son imágenes de pantalla tanto de la TI-89  como de la TI-92. El primer cuadro muestra el cálculo de una antiderivada (integral indefinida) y la descomposición de un polinomio en factores lineales. El segundo cuadro muestra una gráfica de 3 dimensiones, que incluso se puede rotar en tiempo real. El tercer cuadro muestra la solución de un sistema de ecuaciones no lineales, una conversión de unidades físicas, y la conversión del resultado de un cálculo binario al sistema hexadecimal. El cuarto cuadro provee las soluciones numérico / gráfica y algebraica de una ecuación diferencial.

 

 

 

 

 

 

 

 

 

 

 

Tales calculadoras pronto serán la herramienta estándar en la enseñanza de las matemáticas, como lo es la calculadora científica o gráfica hoy en día. En este artículo discuto detalladamente cómo es probable que esta tecnología afecte la enseñanza de las matemáticas. Como introducción, consideraré el papel de la tecnología en general.

 

 

1.2 La tecnología

 

La palabra “tecnología” proviene de la palabra griega technikos que significa “artístico, experto, profesional”. En la forma de computadora, la tecnología se incorpora a más y más áreas de la vida. En esta secuela distingo dos áreas y explico la importancia y la significación de la tecnología en ellas. Las dos áreas son matemáticas (intelectual) y transporte / movimiento (física). Esta comparación fue estimulada por Frank Demana.

 

El método más elemental de transportarse es caminando. El caminar es un logro físico obtenido simplemente con energía muscular. La actividad correspondiente en matemáticas es el cálculo mental (aritmética mental y álgebra mental.) El cálculo mental no requiere nada más que "el poder del cerebro".

 

Montar una bicicleta es otro método de transporte, en el que empleamos un dispositivo mecánico para hacer un uso más eficaz de nuestra energía muscular. Comparado con el caminar,  podemos movernos mayores distancias o hacerlo más rápidamente. La actividad correspondiente en matemáticas es el cálculo de papel y lápiz. Utilizamos el papel y el lápiz como una "memoria externa" que permite que utilicemos nuestro poder cerebral más eficientemente.

 

Otro método de transporte es conducir un automóvil. El automóvil es un dispositivo complejo que produce movimiento. El conductor no necesita (casi) ninguna energía muscular para conducir, pero sí de nuevas habilidades. Debe poder encender el motor, acelerar, dirigir, frenar, apegarse a las regulaciones de tráfico, etc. La actividad correspondiente en matemáticas es el cálculo con la computadora / calculadora. La calculadora o la computadora producen el resultado, mientras que su usuario necesita saber operarlas.

 

¿Cuál método de transporte es pertinente en una situación dada? Si pedimos a un colega que nos traiga un periódico desde un kiosco de revistas distante 250 metros, él probablemente caminará. En caso de que el kiosco esté a 1 000 metros, una bicicleta puede ser el medio de transporte más razonable. En caso de que la distancia al kiosco sea de 10 000 metros, uno utilizará un automóvil. En matemáticas, el uso sensible de la tecnología es consecuente: la multiplicación de dos números de un dígito es mejor hacerla mentalmente. Cuando se multipliquen dos números de dos dígitos puede ser mejor usar papel y lápiz, mientras que para obtener el producto de dos números de cinco cifras uno utilizará una calculadora.

 

Uno podría objetar que “muchos estudiantes utilizarán una calculadora para obtener el producto de 7 y 9”, y por lo tanto es muy probable que pierdan la habilidad de realizar aritmética mental. Éste es un caso claro del uso impropio de la tecnología, lo que sucede no solamente en matemáticas. Alguna gente emplea inapropiadamente su automóvil conduciendo 250 metros hasta el kiosco de periódicos más cercano. Los que actúan de este modo se dañan en principio a sí mismos  (carencia de ejercicio físico) y también a nuestro ambiente (mediante los gases del escape). A pesar del posible uso inapropiado del automóvil no exigimos su prohibición. Análogamente, tampoco debemos prohibir las calculadoras y las computadoras sólo porque algunos estudiantes puedan utilizarlas incorrectamente. Así como hemos necesitado (y aún necesitamos) crear la conciencia general de que el ejercicio físico es esencial para tener un buen físico y salud, necesitamos también crear la conciencia de que los ejercicios intelectuales (la aritmética mental y el álgebra mental son tales ejercicios) son esenciales para la aptitud y la salud intelectuales. Volveremos sobre esta discusión en la última pero más importante sección.

 

La analogía no se acaba todavía. ¿Y si el colega a quien le pedimos traer el periódico desde un kiosco ubicado a  250 metros no puede caminar correctamente (por ser discapacitado o tener una pierna quebrada)? Para él, caminar 250 metros puede ser muy difícil, si no es que imposible. Hay tecnología disponible para ayudar a la gente en estas circunstancias, por ejemplo una silla de ruedas. Usar una silla de ruedas es un método de transporte apoyado en tecnología, en el que se compensa una deficiencia física. En la actividad intelectual las deficiencias podrían también ocurrir, y su compensación es  deseable si no es que necesaria. Doy un ejemplo tomado de la enseñanza de las matemáticas. Un estudiante con deficiencias en la resolución de sistemas de ecuaciones lineales encontrará difíciles los problemas de la geometría analítica, simplemente porque el resolver un sistema de ecuaciones es un subproblema que encontrará con frecuencia en geometría analítica. Es no solamente un acto de humanidad, sino nuestro deber pedagógico proveer a este estudiante de una herramienta que compense su deficiencia, permitiendo por lo tanto que el estudiante pueda hacer geometría analítica correctamente a pesar de su deficiencia.

 

Como demostraremos más adelante con más ejemplos, las calculadoras y las computadoras pueden ser excelentes herramientas matemáticas de  compensación que permiten que los estudiantes menos dotados puedan abordar tópicos avanzados. Es evidente que la  meta final en la enseñanza de las matemáticas consiste en eliminar todas las deficiencias en aquellas habilidades que son consideradas como esenciales. Una persona físicamente discapacitada no necesariamente tiene  que estar atada a una silla de ruedas por el resto de su vida. Un médico se esforzará por reparar una inhabilidad física de su paciente tanto como sea posible, con una terapia individual. De manera semejante, un profesor debe esforzarse en reparar una discapacidad intelectual / matemática de sus estudiantes con una terapia apropiada, individual. En ambos casos, facilitaremos la  “vida cotidiana con la discapacidad” del paciente, es decir, el tiempo fuera de la terapia, proporcionando una herramienta de compensación apropiada (silla de ruedas, calculadora).

 

Lo que sigue es un resumen de la analogía que hemos discutido.

 

 

 

 

 

2. Enseñando con tecnología

 

De acuerdo con lo que explicamos en la sección anterior, distinguimos dos aplicaciones elementales de las calculadoras o computadoras en la enseñanza: automatización y compensación. Basándonos en estos dos tipos de usos, demostramos cómo uno puede utilizar las calculadoras y  computadoras como valiosas herramientas de enseñanza, examinando cuatro asuntos que pienso son especialmente importantes en la enseñanza de las matemáticas: trivialización, experimentación, visualización, y concentración.

 

2.1 Trivialización

 

El automóvil ensanchó nuestros “horizontes de transporte”, trivializando el movimiento hasta ciertas distancias. Semejantemente, la calculadora ensanchó nuestros “horizontes de cálculo”.

 

¿Recuerda usted los “viejos tiempos” antes de las calculadoras científicas? Las preguntas del examen o las tareas tenían que ser elegidas muy cuidadosamente, de modo que todos los resultados intermedios y finales fueran “agradables”. Un resultado “agradable” era un número entero, una fracción simple, o un radical simple que, más adelante en el cálculo, desaparecería con frecuencia. Esto era importante, ya que de otro modo los estudiantes habrían tenido que utilizar la mayoría de su tiempo realizando operaciones aritméticas. Con una calculadora científica uno puede multiplicar dos números de siete dígitos tan rápidamente como lo hace con dos números de un dígito. La calculadora científica trivializa la ejecución de operaciones aritméticas.

 

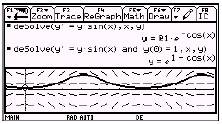
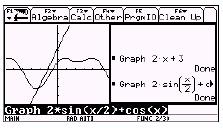
Trazar la gráfica de una función lineal (por ejemplo, ) es simple una vez que usted conoce el significado geométrico de los dos coeficientes. Una pizca de talento y una regla son suficientes para producir una gráfica apropiada. El trazado de la gráfica de una función como  es mucho más difícil y la producción de una gráfica apropiada requiere de una dosis razonable de talento para dibujar. Con una calculadora gráfica uno puede graficar ambas funciones empleando la misma cantidad de tiempo y talento. La calculadora gráfica trivializa la producción de gráficas.

 

 

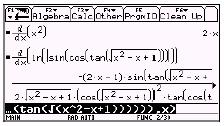
Calcular la primera derivada de  es simple una vez que usted conoce la regla de derivación para las potencias. Sin embargo, calcular la primera derivada de  es mucho trabajo, incluso para un buen matemático. La calculadora algebraica puede manejar ambos ejemplos en segundos. La calculadora algebraica trivializa los cómputos (simbólicos) algebraicos. Un artículo básico sobre la trivialización del cómputo algebraico en la enseñanza de las matemáticas es el de  Buchberger (1989), donde se introduce el principio de Caja Blanca/Caja Negra.

 

 

El automóvil (es decir, la trivialización del movimiento y del transporte) hizo fácilmente manejable una distancia como la de Los Ángeles a San Diego. En otras palabras, algunos problemas de transporte y movimiento que eran considerados difíciles en épocas anteriores, hoy en día constituyen una tarea rutinaria con los automóviles. Semejantemente, la presencia de calculadoras y computadoras en la enseñanza (es decir, la trivialización de la aritmética, las gráficas y el álgebra) implica que podemos abordar

 

§         problemas (más) complejos, y

§         problemas (más) realistas.

 

 

 

2.2 Experimentación

 

¿Cómo hemos descubierto todo el conocimiento matemático que poseemos hoy, y cómo encontramos más conocimiento matemático? Según una de las teorías de orientación epistemológica, uno puede visualizar los pasos principales de estos descubrimientos como sigue: La aplicación de algoritmos conocidos produce ejemplos. A partir de los ejemplos observamos las propiedades, que se expresan como conjeturas. Probar una conjetura genera un teorema, es decir, conocimiento garantizado. El conocimiento algorítmicamente útil de los teoremas se pone en ejecución en un nuevo algoritmo. Entonces el algoritmo se aplica a nuevos datos, generando nuevos ejemplos, que conducen a nuevas observaciones...

 

 

 

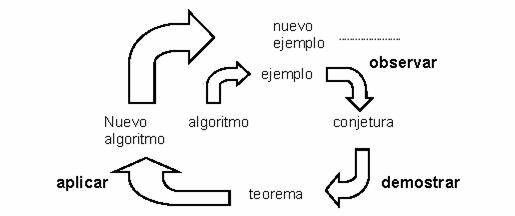
Este esquema en espiral que muestra la trayectoria del descubrimiento del conocimiento (matemático) fue propuesto por Bruno Buchberger. Una descripción detallada de la espiral de la creatividad de Buchberger y referencias a otros modelos relacionados se puede encontrar en el libro (en lengua alemana) altamente recomendado de Heugl, Klinger y Lechner (1996).

 

En esta espiral encontramos tres fases. Durante la fase de experimentación uno aplica algoritmos conocidos para generar ejemplos, después obtiene conjeturas a través de la observación. Durante la fase de verificación las conjeturas se convierten en teoremas mediante el método de la demostración, y entonces el conocimiento algorítmico útil se pone en ejecución en forma de  algoritmos. Durante la fase de uso uno aplica algoritmos a datos verdaderos o ficticios. Típicamente, la resolución de problemas reales responde al propósito de dominar o de facilitar la vida, mientras que la resolución de problemas ficticios responde a un propósito de entretenimiento / diversión (rompecabezas mentales), o al  de encontrar nuevo conocimiento (es decir, a la satisfacción de la curiosidad científica).

 

Las matemáticas tienen ya cerca de 5 000 años de antigüedad. En sus primeros 2 500 años fueron una ciencia experimental y pertenecieron al legado cultural de los egipcios y de otras civilizaciones antiguas. Usando las nociones antedichas, tales matemáticas consistieron solamente de las fases de experimentación y aplicación. Cerca de 500 A.C. los griegos tomaron las matemáticas egipcias y aplicaron a ellas los métodos deductivos de su filosofía (es decir, agregaron la fase de verificación), estableciendo de este modo las matemáticas como la ciencia deductiva que conocemos hoy. A partir de entonces la matemática científica abarcó las tres fases. Después de que el conocimiento matemático creciera por un largo período, un grupo constituido alrededor del matemático francés Dieudonné (el grupo se conoció bajo el  seudónimo de Bourbaki) emprendió un proyecto  que tenía como objetivo reescribir  el conocimiento matemático de su tiempo en una manera uniforme y sucinta. Desarrollaron el sistema de definición–teorema–demostración–corolario..., que ha llegado a ser característico de las matemáticas modernas. Este sistema de Bourbaki, que fue desarrollado con el fin de servir a la comunicación intra matemática, no documentó la fase de la experimentación, por lo tanto consistió solamente de las fases de verificación y aplicación.

 

Gradualmente, el bourbakismo se incrustó en la enseñanza y el aprendizaje. Ha llegado a ser costumbre enseñar matemáticas presentando deductivamente el conocimiento matemático, y luego pidiendo a los estudiantes  que lo aprendan y lo usen / apliquen en la resolución de problemas de tarea y en los exámenes. Es como si uno tuviera que aprender a caminar (o a montar en bicicleta, o a  bailar...)  por medio de estudiar, entender, y después aplicar las descripciones científicas de los movimientos de los músculos requeridos para caminar (o para montar en bicicleta, o para bailar...) en vez de aprender por ensayo y error (es decir, por experimentación), como se hace naturalmente. La mayoría de las teorías sicológicas del aprendizaje de hoy consideran al aprendizaje como un proceso inductivo en el cual la experimentación desempeña un papel importante. Esta es la razón por la cual Freudenthal exigía que no enseñáramos a los estudiantes algo que ellos podrían descubrir por sí mismos (véase Freudenthal, 1979).

 

Difícilmente cualquier matemático en este planeta podría llevar a cabo la investigación matemática  a la manera que exigimos que nuestros estudiantes la hagan. Un estudiante tiene que construir “localmente” su “casa individual de las matemáticas”. Un científico hace justamente lo mismo a escala  “global”, es decir, a una escala mucho mayor. Tanto para el científico como para el estudiante una parte substancial de la adquisición del conocimiento sucede durante la fase de experimentación. Desde este punto de vista, llega a ser comprensible por qué tantos estudiantes están en imposibilidad de comprender las matemáticas, y uno exigiría que la experimentación obtuviera su debida posición dentro de la enseñanza de las matemáticas. ¡La fase de experimentación debe complementar los métodos de enseñanza tradicionales, no substituirlos! No abogamos por la vuelta a las matemáticas experimentales egipcias. Simplemente, la enseñanza de las matemáticas debe pasar por las tres fases de la espiral antedicha.

 

Sin embargo, es comprensible que, en el marco de los currícula actuales, a duras penas haya en ellos alguna experimentación en el sentido de la espiral de la creatividad de Buchberger. Esta clase de experimentación, realizada con papel y el lápiz, consume demasiado tiempo y es proclive al error. Dentro del tiempo disponible en la escuela, los estudiantes podrían producir solamente un número muy pequeño de ejemplos con el fin de observar y descubrir, y un porcentaje elevado de estos ejemplos podría ser fallido debido a los errores de cálculo. ¡No hay nada que usted pueda observar a partir de unos pocos ejemplos, en parte incorrectos! A partir de ahora, las calculadoras algebraicas permiten a los estudiantes experimentar dentro de casi todos los tópicos tratados en la enseñanza de las matemáticas. No hay límite al número de ejemplos que el estudiante puede examinar, y el ayudante electrónico garantiza la pertinencia de los resultados. Hablando de ayudantes: los documentos históricos indican que algunos de los grandes matemáticos, como Carl Friedrich Gauss, emplearon equipos de “calculadoras humanas”, sin los cuales no habrían hecho la mayoría de sus famosos descubrimientos.

 

El gran genio Johann Wolfgang Goethe clamó por “aprender haciendo y observando”. Usando las calculadoras algebraicas podemos ahora realizar el sueño de Goethe.

 

 

2.3 Visualización

 

La visualización significa la ilustración de un objeto, de un hecho o de un proceso. El resultado puede ser gráfico, numérico o algebraico. Hoy, el término se utiliza sobre todo para las ilustraciones gráficas de objetos o de hechos algebraicos o numéricos (el término se utiliza tanto para el proceso de ilustración, como para el resultado del proceso de ilustración). La visualización como técnica de enseñanza de las matemáticas ha llegado a ser importante sobre todo en los países en donde las calculadoras gráficas se utilizan extensamente. Hoy se le usa principalmente para desarrollar la capacidad de alternar entre diferentes representaciones, sobre todo con el fin de estudiar la correspondencia entre las representaciones algebraicas y gráficas. Un ejemplo típico consiste en estudiar cómo el parámetro   afecta la forma de la gráfica de la función .

 

 

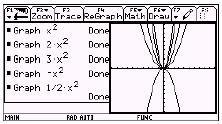
Frank Demana y Bert Waits son los abogados líderes de un estilo de enseñanza conocido como  “el poder de la visualización” (véase Demana y Waits 1990, 1992, 1994).

 

En la sicología del aprendizaje, los científicos descubrieron el concepto de refuerzo y mostraron que los efectos del refuerzo son mejores si éste sigue a la acción inmediatamente. Un ejemplo tomado de la vida diaria es el de un niño que pone su mano sobre una estufa caliente. El dolor inmediato es el mejor requisito previo para que el niño aprenda que no debe hacer esto más. Si el dolor fuera experimentado varios minutos después, el niño probablemente no lo asociaría (durante un largo período) con el contacto con la estufa caliente, y probablemente no aprendería de ello.

 

Al usar una calculadora como herramienta para la visualización, la retroalimentación inmediata es de importancia central. Si usted introduce en su calculadora, por ejemplo, x^2, y después presiona la tecla apropiada, la gráfica correspondiente aparece unas fracciones de segundo después. El cuadro resultante se puede discutir, la gráfica se puede asociar con la expresión, etc. Considere a un estudiante menos dotado y compare el resultado de su  aprendizaje cuando el estudiante tiene que dibujar la gráfica manualmente y cuando se le permite utilizar una calculadora: una gráfica manualmente producida tomaría demasiado tiempo y probablemente tendría solamente una vaga semejanza con la gráfica apropiada. (¿Qué es lo que puede usted observar a partir de ejemplos incorrectos?) Solamente con ayuda de la calculadora este estudiante tiene una oportunidad real de asimilar la correspondencia entre la expresión algebraica y la gráfica (¡apropiada!). Ciertamente, producir gráficas con papel y lápiz continúa siendo una actividad valiosa que es importante para entender la correspondencia entre las representaciones algebraicas y las gráficas. Sin embargo, la inmediatez y la corrección son también factores sicológicos cruciales, de manera que proveer a los estudiantes menos dotados con una herramienta apropiada (tal como una calculadora gráfica) es un deber pedagógico.

 

El hecho de que el profesor utilice o no una herramienta para apoyar una actividad y el cómo lo haga dependen de las metas pedagógicas relacionadas con la actividad. Helmut Heugl afirmó una vez que “si no es pedagógicamente necesario utilizar una calculadora algebraica, entonces es pedagógicamente necesario no utilizar la calculadora algebraica”. Esto significa, en particular, que el profesor resulta  más y más importante en una enseñanza de las matemáticas apoyada por tecnología, y que por lo tanto crece la importancia del entrenamiento de los profesores en servicio y de los futuros profesores.

 

 

2.4 Concentración

 

Podemos comparar la enseñanza y el aprendizaje de las matemáticas con la construcción de una casa, la “casa de las matemáticas”. Los tópicos que enseñamos y las dependencias entre ellos son comparables a los pisos de una casa. Antes de que uno pueda construir el  segundo piso tiene que terminar el primero. De manera semejante, el tratamiento de casi cualquier tópico matemático requiere del dominio de los anteriores. Mostraremos esta idea usando el tópico “solución de una ecuación lineal de una incógnita”.

 

Consideremos la ecuación . Uno tiene que transformar esta ecuación a la forma  ... . Esto se logra eligiendo y aplicando una secuencia apropiada de transformaciones equivalentes. Típicamente, se aconseja al estudiante “llevar los términos en  a uno de los lados de la ecuación” y “llevar el resto de los términos al otro lado”. Por lo tanto, comenzamos por sustraer  :

 

 

Después de elegir esta transformación equivalente, la aplicamos a ambos lados de la ecuación, es decir,  tenemos que simplificar:

 

 

Ahora tenemos que elegir otra transformación equivalente, a saber,  

 

 

Y simplificamos otra vez:

 

 

 

Estamos interesados en la práctica de la enseñanza de las matemáticas. En particular, deseamos saber por qué los estudiantes cometen qué errores. Un error típico comienza con el siguiente argumento: “Hay un 3 antes de la variable . Para conseguir librarme del 3 necesito restar 3”. Es muy probable que este estudiante escriba...

 

 

creyendo que la ecuación ha sido resuelta.

 

¿Qué es lo que anda mal y cómo puede la tecnología ayudar a hacerlo mejor? Un análisis de los pasos realizados arriba revela dos tareas que se alternan: (1) la elección de una transformación equivalente y (2) la simplificación de expresiones algebraicas. Aquí, la elección de una transformación equivalente es una tarea de más alto nivel, por cuanto constituye la esencia de la estrategia para encontrar la solución de una ecuación. Es la nueva habilidad que el estudiante tiene que desarrollar al aprender a resolver ecuaciones. La simplificación de expresiones es una tarea de nivel inferior, para la cual el profesor tiene que asumir que el estudiante ha sido suficientemente bien entrenado.

 

 

  Escoger una transformación de equivalencia

Simplificar                                                     

 

 

Este cuadro demuestra que un estudiante, mientras está intentando aprender una nueva habilidad, tiene que interrumpir en varias ocasiones el proceso de aprendizaje para realizar un cálculo. Esto es lo mismo que si uno fuera interrumpido en varias ocasiones durante una partida difícil de ajedrez. De hecho, es incluso peor, porque la interrupción puede influir en el “juego”: una equivocación cometida durante la interrupción, es decir, durante la tarea de nivel inferior, perturba seriamente la tarea de alto nivel y puede evitar que el estudiante aprenda. Esto es exactamente lo que ha conducido a la solución incorrecta  en el ejemplo antedicho. Después de decidir restar 3, el estudiante debe concentrarse completamente en efectuar la resta en ambos lados de la ecuación, “olvidándose” mientras tanto de la razón para elegir esta transformación equivalente. Pero, en realidad, el estudiante comienza la línea siguiente con "" simplemente “porque la transformación  fue elegida para generar “” en el lado izquierdo de la ecuación”. En el nivel más alto de la tarea, el estudiante tiene la impresión (incorrecta) de que  simplificó la ecuación según lo deseado.

 

Este cambio continuo de niveles ocurre inevitablemente en casi todos los tópicos en las matemáticas escolares. Parece ser  que uno de los problemas centrales en la enseñanza de las matemáticas consiste en que los estudiantes tienen que desarrollar una nueva habilidad mientras que todavía continúan practicando una "vieja" habilidad. Usando una calculadora algebraica el proceso de aprendizaje se podría conducir como sigue. Primero introducimos la ecuación.

 

  ¸

 

Luego sigue la introducción de la transformación equivalente (la calculadora aplica automáticamente el operador de substracción a la expresión previa, es decir, a la ecuación como su primer argumento):

 

  ¸

 

La simplificación, es decir, la aplicación de la transformación de equivalencia a ambos lados de la ecuación, fue realizada por la calculadora. Entonces el estudiante elige la transformación de equivalencia siguiente:

 

  ¸

 

Imitemos al estudiante que ha incurrido en la equivocación arriba discutida:

 

   ¸

 

Es evidente que la calculadora simplifica correctamente, por lo tanto, el estudiante recibe una retroalimentación inmediata que le indica que la transformación  no era acertada (es decir, no simplificó la ecuación  a la forma “”).

 

Aquí encontramos otra vez dos argumentos que ya discutimos anteriormente: (1) el estudiante experimenta con posibles transformaciones equivalentes, por lo tanto hay una fase experimental en el aprendizaje, y (2) la inmediatez del resultado de aplicar la transformación concuerda con lo que discutimos en la sección sobre visualización.

 

Un estudiante que desarrolle el ejercicio presentado arriba apoyado en una calculadora algebraica puede concentrarse completamente en la habilidad (de más alto nivel) de elegir una transformación de equivalencia. La habilidad de nivel inferior de realizar la simplificación es ejecutada (por lo menos en ese momento) por la calculadora.

 

 

 

En Kutzler (1998a) doy instrucciones detalladas de cómo utilizar una TI-92 (o TI-89) para enseñar / aprender la resolución de ecuaciones lineales. El acercamiento algebraico antedicho se discute en detalle, así como los acercamientos numérico y gráfico.

 

 

 

3. El método del andamio

 

En la subsección anterior sobre la concentración comparamos la enseñanza de las matemáticas con la construcción de una casa. En el lenguaje de esta metáfora, el problema antedicho de la enseñanza de las matemáticas se traduce al problema de construir un nuevo piso encima de un piso incompleto. Por ejemplo, tan pronto como comenzamos a construir el piso de “elegir una transformación de equivalencia”, el piso de la “simplificación” sigue estando incompleto para muchos de nuestros estudiantes. En la enseñanza de las matemáticas en la escuela simplemente no tenemos tiempo suficiente para esperar hasta que todos los estudiantes hayan terminado todos los pisos inferiores. El plan de estudios obliga al profesor a continuar con el tópico siguiente, independientemente del progreso individual de los estudiantes. Así pues, es obligado preguntarse cómo un estudiante puede construir un piso nuevo encima de uno incompleto.

 

El ejemplo antedicho demuestra cómo sugiero contestar esta pregunta: mientras que el estudiante desarrolla una habilidad de un nivel más alto, la calculadora resuelve todos los subproblemas que requieran de las habilidades de nivel inferior. Usando el lenguaje de la metáfora, la calculadora es como un andamio sobre el piso incompleto.

 

 

Usando el ejemplo de resolver una ecuación lineal, mostramos el uso de una calculadora algebraica como un andamio colocado sobre el piso de la simplificación. En esta secuencia, aplicaremos el método del andamio a otro ejemplo, a saber, la resolución de un sistema de ecuaciones lineales mediante la eliminación gaussiana.

 

Usaremos el sistema  ,  . Primeramente, el estudiante introduce las ecuaciones:

 

 ¸

  ¸

 

La eliminación gaussiana requiere elegir una combinación lineal de las dos ecuaciones, tal que una variable sea eliminada. Esto es lo que necesita ser aprendido. Todo lo demás (simplificación, substitución, resolver una ecuación de una incógnita) son requisitos previos, en los cuales el profesor confía que los estudiantes estén bien entrenados.

 

 

 

 

 

Intentemos eliminar  sumando cuatro veces la primera ecuación y tres veces la segunda ecuación. (Tanto en la TI-92 como en la TI-89 hay una técnica simple para copiar una ecuación previamente introducida a la línea de entrada. No entraremos aquí en detalles).

 

 

4*(primera ecuación)+3*(segunda ecuación)  ¸

 

 

Voila. La variable   desapareció como se requería. ¿Cuál es la práctica de la enseñanza de este tópico en la escuela? Algunos estudiantes eligen la combinación lineal correcta pero, debido a un error de cálculo, la variable no desaparece. Otros estudiantes eligen una combinación lineal incorrecta pero, otra vez debido a un error de cálculo, la variable desaparece (porque “debe” desaparecer.) Para ambos grupos de estudiantes, sus deficiencias en la simplificación algebraica constituyen una piedra de tropiezo hacia el éxito en aprender la técnica básica de la eliminación gaussiana. Son justamente esos estudiantes  quienes se retrasan más y más conforme “más alto” escalan en la casa de las matemáticas.

 

En el ejercicio anterior, la calculadora algebraica es un andamio que compensa cualquier deficiencia de los estudiantes en las habilidades del más bajo nivel, y por lo tanto les ayuda a evitar errores. En el caso de que la meta final de la enseñanza sea hacer que los estudiantes puedan resolver sistemas de ecuaciones (o realizar cualquier otra habilidad B) manualmente (debido a que, por ejemplo, los estudiantes son sometidos a un examen departamental o estatal hacia el final del año escolar), se recomienda realizar los tres pasos siguientes. El primer paso consiste en enseñar y practicar la habilidad A. El segundo paso consiste en enseñar y practicar la habilidad B, mientras que se usa la calculadora algebraica para resolver todos aquellos subproblemas que requieran de la habilidad A (es decir, que el estudiante puede concentrarse completamente en la habilidad B que está aprendiendo). El tercer paso es combinar las habilidades A y B sin ayuda de la tecnología.

 

 

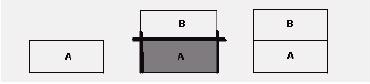
Éste es uno de los muchos métodos concebibles de usar las calculadoras y las computadoras algebraicas como herramientas pedagógicas.

 

El uso temporal de la tecnología puede ayudar a descomponer el proceso de aprendizaje en pedazos “digeribles” más pequeños, más fáciles. Para los estudiantes menos dotados, que no podrían tragar los “pedazos grandes”  que les hemos ofrecido hasta ahora, esta podría ser la única manera de llegar a dominar estos pasos en el aprendizaje. Ellos encuentran más fácil mantener la ruta sin perder de vista los pasos o quedar perdidos (o enredados) en detalles tales como la  simplificación. Al comparar la enseñanza de las matemáticas con la construcción de una casa, el uso de la tecnología se compara con el uso de un andamio.

 

El método del andamio es cualquier secuencia pedagógicamente justificada que decida usar o no usar la tecnología para la trivialización, la experimentación, la visualización o la concentración, tanto en el sentido de la automatización como de la compensación.

 

El uso que aquí se ha presentado de la tecnología como herramienta pedagógica es totalmente independiente de si se le puede o no utilizar durante un examen. El método del andamio tiene como objetivo apoyar el proceso de aprendizaje, es decir, que puede ayudar a alcanzar las metas (tradicionales) de la enseñanza. Aquí, la tecnología es solamente un instrumento para el entrenamiento. Así como un entrenador casero puede ayudarnos a adquirir habilidades físicas, una calculadora algebraica puede ayudarnos a adquirir habilidades intelectuales / matemáticas. Por lo tanto, la tecnología se debe introducir como herramienta pedagógica, independientemente de cualquier cambio al plan de estudios o al esquema de evaluación. Las calculadoras algebraicas pueden ayudar en todos los niveles de las matemáticas en la educación secundaria.

 

En Kutzler  (1998b) describo cómo uno puede utilizar una TI-92 (o una TI-89) para tratar el tópico  “resolución de sistemas de ecuaciones lineales” en la escuela. Además de dar otros detalles sobre el enfoque antedicho, el folleto también describe los métodos numéricos y gráficos, así como el método de substitución.

 

 

 

4. Metas de la enseñanza de las matemáticas

 

Creo que las dos metas centrales en la enseñanza de las matemáticas deben ser entrenar a los estudiantes en dos disciplinas: deportes intelectuales y resolución de problemas.

 

 

4.1 Deportes intelectuales

 

Dada la existencia de las calculadoras algebraicas, Bruno Buchberger planteó la pregunta “¿Por qué deberían los estudiantes aprender las reglas de integración?” (Buchberger, 1989), y Wilfried Herget preguntó: “¿Qué tanta simplificación necesitamos?” ; vea la nota al pie de la página 8 en Hischer (1992). En todas las áreas de la vida necesitamos preguntarnos qué tan lejos debemos llegar en la automatización.

 

Al principio comparamos las matemáticas con el movimiento / transporte. Actualmente, la tecnología del transporte está tan desarrollada que no necesitamos caminar en absoluto en cualquier momento de nuestra vida. Podríamos utilizar las herramientas móviles desde la infancia. Pero no lo hacemos. Sabemos que eso sería devastador para nuestra condición física y nuestra salud: nuestros músculos, puesto que nunca estarían siendo utilizados, degenerarían, y esto afectaría ciertamente al cuerpo entero.

 

Debido a un incremento masivo de la automatización durante los últimos años, muchas de nuestras habilidades intelectuales están en peligro. En el pasado necesitábamos memorizar los números de teléfono; hoy simplemente utilizamos las teclas de memoria de los teléfonos. En el pasado tuvimos que memorizar cómo programar la grabadora de video; hoy simplemente deslizamos un lector de código de barras sobre el programa de la TV. Es evidente que todo esto hace la vida mucho más cómoda. PERO nos lleva a perder lo que yo llamo “aptitud intelectual”. Muchos profesores se quejan de sus estudiantes por la falta de concentración y su baja capacidad de memoria. Éstos son dos síntomas típicos de una salud intelectual en deterioro.

 

En medicina existen definiciones de lo que físicamente debe poder hacer una persona “sana”. Después de un ataque del corazón, por ejemplo, un paciente debe poder caminar cierta distancia y subir las escaleras hasta cierto nivel antes de que se le considere nuevamente sano. Necesitamos algo similar para nuestras capacidades intelectuales, es decir, una definición de lo que debe poder hacer una persona “intelectualmente sana” en términos, por ejemplo, de memorización o de cálculos mentales.

 

Por lo que toca a nuestras capacidades físicas, introdujimos el curso de “Deportes” en la escuela para luchar contra su deterioro progresivo. Necesitamos tomar medidas similares con respecto a nuestras capacidades intelectuales, es decir,  necesitamos introducir en la escuela  el tema de los “deportes intelectuales”. Creo que ésta debe ser una de las metas de la enseñanza de las matemáticas.

 

 

4.1 La resolución de problemas

 

En matemáticas, considero que la resolución de problemas consiste en la capacidad de utilizar las herramientas matemáticas para resolver problemas técnicos del mundo real. La característica esencial de la resolución de problemas la constituyen los tres pasos mostrados en la gráfica más abajo. El primer paso consiste en elegir un modelo y traducir el problema real al lenguaje del modelo, lo que requiere entender el problema y apropiárselo (un problema de optimización, por ejemplo, debe ser traducido a una función  que debe ser optimizada y que describe todas las restricciones entre las variables implicadas). El segundo paso consiste en aplicar los algoritmos disponibles para resolver el problema modelo PM, lo que conduce a una solución modelo SM. El tercer paso, finalmente, consiste en traducir la solución modelo a una solución S del mundo real (a menudo, la gente se refiere a esta retraducción como interpretación).

 

 

 

 

 

 

 

 

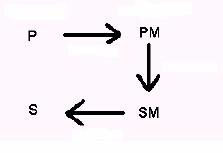
Sin embargo, todavía necesitamos probar que S es realmente una solución de P. En caso de que no lo sea, entonces todo el proceso (es decir, los tres pasos) debe ser repetido, porque el error o  interpretación incorrecta podría estar en cualquier parte: el modelo elegido puede ser inadecuado, la traducción puede ser deficiente, o el cálculo puede ser incorrecto.

 

Hoy, la  resolución de problemas se trata a medias en la escuela. El énfasis principal se pone en el segundo paso, el cálculo, y en su ejecución con papel y lápiz. En consecuencia, la mayoría de los ejercicios de resolución de problemas se tornan en ejercicios para practicar las habilidades de cálculo. Puesto que la traducción difícilmente se enseña de manera explícita, es comprensible que la mayoría de los estudiantes no desarrollen esta capacidad, y que por lo tanto estén temerosos de este tipo de ejercicios. Por consiguiente, la mayoría de los estudiantes creen que tales ejercicios están reservados solamente para los más ingeniosos o inteligentes.

 

Empleando tecnología tan extensamente como sea posible, podemos dedicar mucho más tiempo a enseñar a elegir modelos y a traducir. Una vez que estas habilidades se enseñen explícitamente, más estudiantes las apreciarán y dominarán.

 

 

4.3 El futuro de la enseñanza de las matemáticas

 

El currículo debe tener como objetivo el educar a los estudiantes en las disciplinas de los deportes intelectuales y en la resolución de problemas.

 

El objetivo de los deportes intelectuales es la aptitud y salud intelectuales, como se ha descrito con detalle anteriormente. Es evidente que la tecnología debe ser solamente una herramienta para el entrenamiento (un “entrenador matemático casero”), y no debe ser utilizada al evaluar y examinar estas capacidades.

 

El objetivo de la resolución de problemas es desarrollar la capacidad de usar las herramientas dadas para resolver problemas dados. Es evidente que el uso de la tecnología debe ser aquí ampliamente fomentado.

 

De nuevo esbozaré un paralelo usando la comparación inicial de las matemáticas con el movimiento / transporte. La resolución de problemas se compara con el deseo real de ir de A  a  B (o de transportar algo de A a B). Solamente importa llegar a B. Es menos importante (quizá mucho menos importante) cómo conseguimos llegar allí. Los deportes intelectuales se comparan con un corredor que trota a lo largo de una pista para ganar condición física y salud. Solamente importa la carrera. Es poco importante dónde está la pista o a dónde conduce. Transferido al campo de la enseñanza de las matemáticas esto significa lo siguiente. Al resolver problemas solamente cuenta el resultado. Es irrelevante cómo fueron realizados los cálculos. En los deportes intelectuales solamente importa la ejecución del cálculo, mientras que el resultado es poco importante.

 

 

 

4.4 Evaluación

 

Lo dicho anteriormente nos conduce a una regla muy simple para la evaluación. Al evaluar la aptitud intelectual no se permite ninguna herramienta, ni siquiera una simple calculadora de cuatro operaciones. Al evaluar la resolución de problemas se permiten todas las herramientas (mucho mejor: se requieren), en particular las calculadoras gráficas o algebraicas. En caso de que esta partición no sea manejable dentro de un examen, uno debe evaluar las dos disciplinas en momentos diferentes. Resulta obvio esbozar un paralelo con el patinaje sobre hielo: los deportes intelectuales se comparan con los ejercicios obligatorios, en los cuales el atleta demuestra la maestría alcanzada en la ejecución de las técnicas básicas. La resolución de problemas se compara con los ejercicios libres, en los cuales el atleta demuestra su capacidad de combinar las técnicas básicas en una coreografía agradable. El puntaje total depende de los puntajes de las partes obligatoria y libre.

 

A fin de cuentas, la tecnología debe desempeñar un papel secundario en ambas disciplinas. En los deportes intelectuales la meta es la ejecución con un mínimo de herramientas. En la resolución de problemas la meta es dominar todas las habilidades y capacidades que sean necesarias para resolver problemas, y que no son proporcionadas por ninguna tecnología en particular. Una buena enseñanza de las matemáticas utilizará la calculadora o la computadora como la enseñanza de la lengua utiliza los diccionarios.

 

 

 

5 Observaciones finales

 

William Shakespeare dijo una vez: “Nada es bueno o malo, solamente el pensamiento lo hace tal”. Considerando la tecnología para la enseñanza de las matemáticas uno puede cambiar esta frase por la siguiente: “las calculadoras y las computadoras no son ni buenas ni malas herramientas de enseñanza, solamente el uso las convierte en tales”. Al conducir un automóvil, lo más importante es el conductor; el automóvil es secundario. Semejantemente, cuando se enseña con tecnología lo más importante es el profesor; la tecnología viene en segundo lugar. Éste es otro argumento a favor de fortalecer el entrenamiento de los profesores en servicio y de los futuros profesores.

 

En Austria en 1991 todas las escuelas generales (Gymnasien) y técnicas (Höhere Technische Lehranstalten) del nivel medio superior fueron equipados con el sistema de álgebra simbólica DERIVE. Al mismo tiempo, se desarrolló un proyecto de investigación que fue conocido como el Austrian DERIVE Project. El proyecto involucró a 800 estudiantes a quienes les fueron enseñadas las matemáticas regulares con DERIVE. Los resultados fueron publicados en el libro en lengua  alemana de Heugl, Klinger y Lechner (1996), y se puede también encontrar la publicación en lengua inglesa  (Aspetsberger y Fuchs, 1996). En el año académico 1997/98, el mismo equipo desarrolló el Austrian TI-92 Project con 2 000 estudiantes usando la TI-92 en sus clases regulares de matemáticas. Los resultados se pueden encontrar en Internet en la dirección http://www.acdca.ac.at. Otro proyecto TI-92 está actualmente en marcha con la participación de 3 000 estudiantes.

 

Las investigaciones austriacas y muchas otras investigaciones mostraron lo siguiente: Si la tecnología se utiliza adecuadamente, ello conduce a

 

§         una enseñanza y aprendizaje más eficientes,

§         una actividad del estudiante más productiva e independiente,

§         más creatividad del estudiante,

§         una importancia creciente del profesor.

 

El profesor tiene el deber de acompañar y conducir a los estudiantes en su viaje, en parte individual, de descubrimiento a través del mundo de las matemáticas. Por lo tanto, la clave del éxito en la enseñanza de las matemáticas es un buen entrenamiento de los profesores. La tecnología por sí misma no cambia la enseñanza, pero es un catalizador para que los profesores cambien sus métodos y enfoquen la enseñanza en conceptos y habilidades, teniendo como objetivo una mejor enseñanza de las matemáticas.

 

 

En caso de que usted tenga preguntas o sugerencias, escríbame por favor a b.kutzler@eunet.at. Una colección de información regularmente puesta al día sobre tecnología en la enseñanza de las matemáticas se puede encontrar en www.kutzler.com.

 

Gracias especiales a Vlasta Kokol-Voljc por su retroalimentación y valiosas sugerencias.

 

 

 

Referencias

K Aspetsberger, K Fuchs, 1996 (guest editors): The International DERIVE Journal Vol 3, No. 1. (The whole issue was dedicated to the Austrian DERIVE project.) Hemel Hempstead:Research Information Ltd., 106 pages, ISSN 1351-0789.

B Buchberger, 1989: Why Should Students Learn Integration Rules? RISC-Linz Technical Report no. 89-7.0, Univ. of Linz, Austria.

F Demana, B Waits, 1990: The Role of Technology in Teaching Mathematics. In: „The Mathematics Teacher“, National Council of Teachers of Mathematics, vol. 82, no. 1.

F Demana, B Waits, 1992: A Computer for All Students. In: „The Mathematics Teacher“, National Council of Teachers of Mathematics, vol. 84, no. 2.

F Demana, B Waits, 1994: Graphing Calculator Intensive Calculus: A First Step in Calculus Reform for All Students. In: „Proc. Of the Preparing for New Calculus Conference“ (ed. A. Solow), Mathematical Association of America.

H Freudenthal, 1979: Mathematik als pädagogische Aufgabe. Klett Studienbücher.

H Heugl, W Klinger, J Lechner, 1996: Mathematikunterricht mit Computeralgebra-Systemen (Ein didaktisches Lehrerbuch mit Erfahrungen aus dem österreichischen DERIVE-Projekt). Bonn:Addison-Wesley, 307 pages, ISBN 3-8273-1082-2.

H Hischer, 1992 (ed): Wieviel Termumformung braucht der Mensch? Proceedings of the 10th Symposium of the Working Group „Mathematics Teaching and Computer Science“ of the Austrian/German Society of Mathematics Education (Gesellschaft für Didaktik der Mathematik e.V.), Sept 25-27, 1992, Wolfenbüttel, Germany, ISBN 3-88120-221-8.

B Kutzler, 1995: Improving Mathematics Teaching with DERIVE. Bromley:Chartwell-Bratt, 185 pages, ISBN 0-86238-422-2 (available in the US from west@trib.com, in the UK from info@ChartwellYorke.com).

B Kutzler, 1996: Introduction to the TI-92 (Handheld Computer Algebra). Hagenberg:bk teachware, 184 pages, ISBN 3-901769-02-1.

B Kutzler, 1998a: Solving Linear Equations with the TI-92 (Experimental Learning / Visualization / Scaffolding Method). Hagenberg:bk teachware, 36 pages, ISBN 3-901769-03-X

B Kutzler, 1998b: Solving Systems of Equations with the TI-92 (Experimental Learning / Visualization /Scaffolding Method). Hagenberg:bk teachware, 44 Seiten, ISBN 3-901769-05-6

 

The last three publications are available in the US from EAI, info@eaiusa.com, in the UK from Chartwell-Yorke, info@ChartwellYorke.com, and worldwide from the publisher bk teachware, info@bkteachware.com.